Fractales; aberraciones matemáticas, bellezas naturales
- artscienceandstuff

- 24 sept 2021
- 7 Min. de lectura
Por: José Alberto Galicia Delgado
"El universo es fractal. Cuanto más lo miras más interesante se vuelve" John Lloyd
Desde niños siempre tocamos, observamos y aprendemos de qué forma y aspecto es aquello que nos rodea, la geometría es una de las tantas herramientas que nos permite comprender el mundo a nuestro alrededor. Sin embargo, existe una manera mucho más precisa para describir al mundo: la geometría fractal.
¿Qué es un fractal?
En términos coloquiales, se podría decir que algo fractal, es algo que presenta autosimilaridad en su constitución geométrica, es decir, podemos ver el mismo patrón geométrico repetido una y otra vez. Imaginemos pues cualquier forma que se repite a sí misma conforme la vemos más de cerca, ¿que pasaría si te dijera que el resto del mundo se construye del mismo modo? Por ejemplo, las ramas de los árboles y la forma en que se desarrollan es una forma en que podemos ver fractales más cotidianamente, pues de cada una de sus ramas, surgen otras de menor tamaño y así sucesivamente hasta llegar a las hojas. Lo mismo ocurrirá si miramos las hojas compuestas de una jacaranda o las frondas de un helecho.
Fig. 1 Jacaranda y helecho
El copo de nieve de Koch
Supongamos que tenemos un triángulo equilátero al que le añadimos uno más en cada lado, a este nuevo le añadimos otro triángulo en cada lado y así sucesivamente de manera indefinida. Si lo observamos con una lupa o un microscopio, veríamos exactamente lo mismo, triángulo sobre triángulo. La figura resultante se conoce cómo curva de Koch, (pues el contorno es una curva imposible de dibujar), o copo de nieve de Koch.

Fig. 2 Copo de nieve de Koch
Lo interesante de esta figura es que si lo medimos con cualquier herramienta de medición común, por supuesto que su tamaño será finito, pues una regla (por ejemplo) no puede contemplar los triángulos más pequeños, pero, si lo cortásemos por un extremo y lo desdoblamos cómo un hilo, terminaremos con una cantidad infinita de este, pues siempre que desdobláramos un pico habría dentro otro más pequeño que desdoblar, teniendo así a nuestra aberración matemática; un objeto tal que mide apenas poco más área que el triángulo inicial, pero un perímetro infinito.
¿Entonces cómo los clasificamos? La respuesta es…
Midiendo su dimensión. Es decir, todos sabemos que hay objetos unidimensionales, bidimensionales, tridimensionales y demás. Un hilo es unidimensional, una hoja de papel es bidimensional y un cubo tridimensional, pero, ¿si esa hoja de papel se arruga hasta ser una bola sigue siendo bidimensional? o ¿y sí el hilo cubre la superficie de la hoja?, entonces ahí es cuando perdemos la noción de lo que son las dimensiones.
Fig. 3 Hilo y hoja
Para evitar esta incertidumbre y establecer una regla general, en 1919 el matemático Félix Hausdorf introdujo el concepto de dimensión fractal (df) para caracterizar a estos monstruos, de esta forma es posible verificar que un hilo tendría una dimensión uno, una hoja plana una dimensión dos,un cubo una dimensión tres y así sucesivamente hasta que nos topamos con los fractales, lo cuales (*sonidos de sorpresa fingidos*) ¡tienen dimensiones fraccionales y no enteras!, es decir, en el caso del copo de nieve su dimensión es de 1.2619 y es entendible que tenga una dimensión mayor a 1 y menor a 2, pues ocupa más espacio que una recta (df= 1) pero menos que un plano (df=2).
Señores fractales, con traje y corbata
Es en 1975 cuando Benoit Mandelbrot denominó cómo fractales a todas las formas generadas por repetición, con detalle a toda escala, no son diferenciables y tienen dimensión fraccional. Reconociendo a los fractales cómo herramientas para investigar todo tipo de fenómenos físicos, o como conclusiones que surgieron de observar la naturaleza y darse cuenta de que no sólo es más compleja, si no que tiene un nivel diferente, pues, a parte de los observables a simple vista, podemos encontrarlos hasta en los fenómenos aparentemente más azarosos, como en los depósitos o agregados generados por el polvo y esmog, así cómo incluso la formación de cristales y el movimiento de burbujas de aire en los fluidos, según las observaciones de Leonard M. Sander en 1987.
Fig. 4 Benoit Mandelbrot
Redundancia natural
Hay que aclarar que los fractales se presentan en la naturaleza de manera estadística, es decir, no encontraremos fractales que cumplan con exacta precisión la condición igual que los construidos por matemáticos. No es poco común encontrar fractales a simple vista, sólo es necesaria la curiosidad y un ojo que sabe lo que está buscando; les podemos encontrar en las hojas de los helechos, en las hojas compuestas de los árboles, los bordes de una nube, el margen aserrado de un bosque, el perfil de una montaña, las semillas del girasol, hojas delicadamente ordenadas de una suculenta o hasta en las espinas de un cactus.

Fig. 5 fractales en la naturaleza
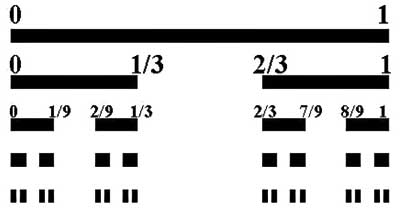
También podemos encontrar fractales en niveles mayores, incluso llegando al orden de las galaxias, sorprendentemente, la distribución de estrellas, la distribución de los anillos de saturno, las variaciones del nivel del agua en el río Nilo, entre otras cosas, se acoplan a un modelo basado en el fractal conjunto de Cantor, el cual se crea de forma muy sencilla: tomamos una recta y la dividimos en tres Representación del conjunto de Cantor en partes iguales, extraemos la de en medio y repetimos lo mismo con las dos partes restantes de manera indefinida. Este fractal fue usado por primera vez cuando se generó con el un modelo de la aparición de ruido en líneas de comunicación (las interrupciones que solemos escuchar al hablar por teléfono o escuchar el radio), que aparecen de forma intermitente y así existen diversos ejemplos y fenómenos explicables con esta geometría, conociéndose incluso la dimensión fractal de casi cada tipo de roca y material en el planeta.
Fig. 5 Fractales en escala macro y el conjunto de Cantor
También los encontramos dentro de nuestro propio cuerpo; redes neuronales, todo tipo de vasos, el árbol pulmonar y muchos de nuestros ciclos biológicos, presentan dimensión fractal. En la mayoría de estos casos, dicha estructura se refleja cómo una ventaja evolutiva, pues permite mayor área de contacto con el medio en un volumen mucho menor al esperado, por lo tanto, provee mayor probabilidad de alimentarse, mayor captación de luz solar, mayor captación de oxígeno, más atractivo visual, mejor empaquetamiento (cómo en el caso de algunas semillas), entre otras, por lo cual es perfectamente razonable que la naturaleza haya preferido estas formas por encima de otras.

Fig. 6 Redes neuronales
Fractales ¿Para qué?
En el campo de la geología y geofísica nos encontramos con un uso muy curioso y es que, al ocurrir un impacto de un meteorito, una explosión o un choque entre dos rocas los fragmentos coinciden con la condición de fractales, es decir, presentan patrones de tamaño-distribución, diámetro-longitud similares (entre otros), lo cual ocurre en todas las escalas. Es decir, si por ejemplo, al quebrar un cubo se divide en 8 partes iguales, probablemente cada una de esas partes se fragmentarán del mismo modo cuando sean quebradas, con estos datos se pueden realizar estudios sobre materiales y efectos de fenómenos naturales sobre estos.
Fig. 7 Fractales en las playas y en el choque de meteoritos
También se sabe que la localización de un epicentro en un temblor se distribuye de manera fractal. Igualmente sirven para analizar estructuras que no tienen una escala de longitud definida, un ejemplo usado comúnmente son las líneas de costa; si viésemos dos playas desde el cielo, con escalas diferentes (1:10 y 1:100 km, por ejemplo) pero no supiéramos en qué escala se observan, no podríamos identificar cuál pertenece a cada una, pues lucen iguales sin importar la escala a la que se observen, este es también, un perfecto ejemplo de autosimilaridad, pues cada una de las partes es igual al todo y por esto vemos lo mismo a cualquier escala. Muchos procesos tecnológicos están basados en fractales, tal como el almacenamiento y reproducción de imágenes o el análisis de los ritmos biológicos (ej: ritmo cardíaco), incluso se estudian para el diseño de nuevos nanomateriales con funciones peculiares cómo la recolección de agua.
Fractales en el mundo artístico
Por otro lado, según el enfoque de estudio, existen distintas definiciones de fractales, cada una con sus fórmulas matemáticas y escalas de medición, pero todas cumplen con el deleite al ojo humano en la búsqueda de patrones y similitud entre partes, siendo esto un tanto curioso, pues las investigaciones sugieren que son estéticamente más atractivos y los preferimos por encima de otras formas geométricas. Es por esto que quizá, ciertos artistas se inclinan a formas estéticas estrechamente relacionadas, tal cómo algunos cuadros de Jackson Pollock, los cuáles han sido analizados por expertos, encontrando que presentan una espectros fractales muy similares, lo cual es sorprendente porque todos estos cuadros fueron pintados en diferentes circunstancias, así como también se encontró que la dimensión fractal de sus cuadros se fue aproximando a 2 conforme pasaron los años, incluso proponiéndose la dimensión fractal cómo una variable para autentificar pinturas.
Fig. 8 Jackson Pollock
Otro caso famoso es el de las obras de Yayoi Kusama, cuyas pinturas que han sido realizadas con patrones de puntos fueron analizadas y sorprendentemente tienen una dimensión fractal muy similar a la de Pollock, pero tienen una complejidad mayor. Así que, sin duda, los fractales se esconcen incluso en donde creemos que no los hay; desde algo tan aparentemente amorfo cómo una nube, algo invisible al ojo humano cómo una señal de radio, algo tan extravagante cómo una pintura de Pollock o algo tan vasto cómo los anillos de saturno, por lo que seguramente quedan muchos por estudiar, modelos que desarrollar y obras de arte que crear con ellos.
Fig. 9 Yayoi Kusama
Referencias
· Barnsley, M. F. (2014). Fractals everywhere. Academic press.
· Branka Spehar; Colin W.G. Clifford; Ben R. Newell; Richard P. Taylor (2003). Universal aesthetic of fractals. , 27(5), 813–820. doi:10.1016/s0097-8493(03)00154-7
· Bunde, A., & Havlin, S. (Eds.). (2013). Fractals in science. Springer
· Corbalán F., (2017), Las matemáticas escondidas detrás de las pinturas de Jackson Pollock. ABC. https://www.abc.es/ciencia/abci-matematicas-escondidas-detras-pinturas-jackson-pollock-201712180942_noticia.html
· De la Calleja, E. M., Cervantes, F., & De la Calleja, J. (2016). Order-fractal transitions in abstract paintings. Annals of Physics, 371, 313-322.
· de la Calleja, E., & Zenit, R. (2020). Fractal dimension and topological invariants as methods to quantify complexity in Yayoi Kusama's paintings. arXiv preprint arXiv:2012.06108.
· Feder, J. (2013). Fractals. Springer Science & Business Media.
· Sander, L. M. (1987). Fractal growth. Scientific American, 256(1), 94-101.
· Spehar, Branka; Rogowitz, Bernice E.; Pappas, Thrasyvoulos N.; Taylor, Richard P.; de Ridder, Huib (2013). SPIE Proceedings [SPIE IS&T/SPIE Electronic Imaging - Burlingame, California, USA (Sunday 3 February 2013)] Human Vision and Electronic Imaging XVIII - Fractals in art and nature: why do we like them?. , 8651(), 865118–. doi:10.1117/12.2012076
· Talanquer, V. A. (2011). Fractus, fracta, fractal: fractales, de laberintos y espejos. Fondo de cultura económica.
· Turcotte, D. L. (1986). Fractals and fragmentation. Journal of Geophysical Research, 91(B2), 1921–. doi:10.1029/jb091ib02p01921


































Comentarios